Global Positioning System

Geodesy
Fundamentals
Geodesy · Geodynamics
Geomatics · Cartography
Concepts
Datum · Distance · Geoid
Figure of the Earth
Geodetic system
Geog. coord. system
Hor. pos. representation
Map projection
Reference ellipsoid
Satellite geodesy
Spatial reference system
Technologies
GNSS · GPS · ...
Standards
ED50 · ETRS89 · NAD83
NAVD88 · SAD69 · SRID
UTM · WGS84 · ...
History
History of geodesy
NAVD29 · ...

The Global Positioning System (GPS) is a space-based satellite navigation system that provides location and time information in all weather, anywhere on or near the Earth, where there is an unobstructed line of sight to four or more GPS satellites. It is maintained by the United States government and is freely accessible by anyone with a GPS receiver. The system imposes some technical limitations which are only removed for authorized users.

The GPS program provides critical capabilities to military, civil and commercial users around the world. In addition, GPS is the backbone for modernizing the global air traffic system.

The GPS project was developed in 1973 to overcome the limitations of previous navigation systems,[1] integrating ideas from several predecessors, including a number of classified engineering design studies from the 1960s. GPS was created and realized by the U.S. Department of Defense (DoD) and was originally run with 24 satellites. It became fully operational in 1994.

Advances in technology and new demands on the existing system have now led to efforts to modernize the GPS system and implement the next generation of GPS III satellites and Next Generation Operational Control System (OCX).[2] Announcements from the Vice President and the White House in 1998 initiated these changes. In 2000, U.S. Congress authorized the modernization effort, referred to as GPS III.

In addition to GPS, other systems are in use or under development. The Russian GLObal NAvigation Satellite System (GLONASS) was in use by only the Russian military, until it was made fully available to civilians in 2007. There are also the planned European Union Galileo positioning system, Chinese Compass navigation system, and Indian Regional Navigational Satellite System.

Contents

History

The design of GPS is based partly on similar ground-based radio-navigation systems, such as LORAN and the Decca Navigator developed in the early 1940s, and used during World War II. In 1956, Friedwardt Winterberg[3] proposed a test of general relativity (for time slowing in a strong gravitational field) using accurate atomic clocks placed in orbit inside artificial satellites. (To achieve accuracy requirements, GPS uses principles of general relativity to correct the satellites' atomic clocks.[4]) Additional inspiration for GPS came when the Soviet Union launched the first man-made satellite, Sputnik in 1957. Two American physicists, William Guier and George Weiffenbach, at Johns Hopkins's Applied Physics Laboratory (APL), decided on their own to monitor Sputnik's radio transmissions. They soon realized that, because of the Doppler effect, they could pinpoint where the satellite was along its orbit from the Doppler shift. The Director of the APL gave them access to their brand new UNIVAC II to do the heavy calculations required. When they released the orbit of Sputnik to the media, the Russians were dumbfounded to learn how powerful American computers had become, as they would not have been able to calculate the orbit themselves. The following spring, Frank McClure, the deputy director of the APL, asked Guier and Weiffenbach to look at the inverse problem where you know the location of the satellite and you want to find your own location. (The Navy was developing the submarine-launched Polaris missile, which required them to know the submarine's location.) This led them and APL to develop the Transit system.[5]

The first satellite navigation system, Transit (satellite), used by the United States Navy, was first successfully tested in 1960. It used a constellation of five satellites and could provide a navigational fix approximately once per hour. In 1967, the U.S. Navy developed the Timation satellite that proved the ability to place accurate clocks in space, a technology required by GPS. In the 1970s, the ground-based Omega Navigation System, based on phase comparison of signal transmission from pairs of stations,[6] became the first worldwide radio navigation system. Limitations of these systems drove the need for a more universal navigation solution with greater accuracy.

While there were wide needs for accurate navigation in military and civilian sectors, almost none of those were seen as justification for the billions of dollars it would cost in research, development, deployment, and operation for a constellation of navigation satellites. During the Cold War arms race, the nuclear threat to the existence of the United States was the one need that did justify this cost in the view of the United States Congress. This deterrent effect is why GPS was funded. It is also the reason for the ultra secrecy at that time. The nuclear triad consisted of the United States Navy's submarine-launched ballistic missiles (SLBMs) along with United States Air Force (USAF) strategic bombers and intercontinental ballistic missiles (ICBMs). Considered vital to the nuclear deterrence posture, accurate determination of the SLBM launch position was a force multiplier.

Precise navigation would enable United States submarines to get an accurate fix of their positions prior to launching their SLBMs.[7] The USAF with two-thirds of the nuclear triad also had requirements for a more accurate and reliable navigation system. The Navy and Air Force were developing their own technologies in parallel to solve what was essentially the same problem. To increase the survivability of ICBMs, there was a proposal to use mobile launch platforms (such as Russian SS-24 and SS-25) and so the need to fix the launch position had similarity to the SLBM situation.

In 1960, the Air Force proposed a radio-navigation system called MOSAIC (MObile System for Accurate ICBM Control) that was essentially a 3-D LORAN. A follow-on study called Project 57 was worked in 1963 and it was "in this study that the GPS concept was born." That same year the concept was pursued as Project 621B, which had "many of the attributes that you now see in GPS"[8] and promised increased accuracy for Air Force bombers as well as ICBMs. Updates from the Navy Transit system were too slow for the high speeds of Air Force operation. The Navy Research Laboratory continued advancements with their Timation (Time Navigation) satellites, first launched in 1967, and with the third one in 1974 carrying the first atomic clock into orbit.[9]

With these parallel developments in the 1960s, it was realized that a superior system could be developed by synthesizing the best technologies from 621B, Transit, Timation, and SECOR in a multi-service program.

During Labor Day weekend in 1973, a meeting of about 12 military officers at the Pentagon discussed the creation of a Defense Navigation Satellite System (DNSS). It was at this meeting that "the real synthesis that became GPS was created." Later that year, the DNSS program was named Navstar. With the individual satellites being associated with the name Navstar (as with the predecessors Transit and Timation), a more fully encompassing name was used to identify the constellation of Navstar satellites, Navstar-GPS, which was later shortened simply to GPS.[10]

After Korean Air Lines Flight 007, carrying 269 people, was shot down in 1983 after straying into the USSR's prohibited airspace,[11] in the vicinity of Sakhalin and Moneron Islands, President Ronald Reagan issued a directive making GPS freely available for civilian use, once it was sufficiently developed, as a common good.[12] The first satellite was launched in 1989, and the 24th satellite was launched in 1994.

Initially, the highest quality signal was reserved for military use, and the signal available for civilian use was intentionally degraded (Selective Availability). This changed with President Bill Clinton ordering Selective Availability to be turned off at midnight May 1, 2000, improving the precision of civilian GPS from 100 meters (330 ft) to 20 meters (66 ft). The executive order signed in 1996 to turn off Selective Availability in 2000 was proposed by the US Secretary of Defense, William Perry, because of the widespread growth of differential GPS services to improve civilian accuracy and eliminate the US military advantage. Moreover, the US military was actively developing technologies to deny GPS service to potential adversaries on a regional basis.[13]

Over the last decade, the U.S. has implemented several improvements to the GPS service, including new signals for civil use and increased accuracy and integrity for all users, all while maintaining compatibility with existing GPS equipment.

GPS modernization [14] has now become an ongoing initiative to upgrade the Global Positioning System with new capabilities to meet growing military, civil, and commercial needs. The program is being implemented through a series of satellite acquisitions, including GPS Block III and the Next Generation Operational Control System (OCX). The U.S. Government continues to improve the GPS space and ground segments to increase performance and accuracy.

GPS is owned and operated by the United States Government as a national resource. Department of Defense (DoD) is the steward of GPS. Interagency GPS Executive Board (IGEB) oversaw GPS policy matters from 1996 to 2004. After that the National Space-Based Positioning, Navigation and Timing Executive Committee was established by presidential directive in 2004 to advise and coordinate federal departments and agencies on matters concerning the GPS and related systems. The executive committee is chaired jointly by the deputy secretaries of defense and transportation. Its membership includes equivalent-level officials from the departments of state, commerce, and homeland security, the joint chiefs of staff, and NASA. Components of the executive office of the president participate as observers to the executive committee, and the FCC chairman participates as a liaison.

The DoD is required by law to "maintain a Standard Positioning Service (as defined in the federal radio navigation plan and the standard positioning service signal specification) that will be available on a continuous, worldwide basis," and "develop measures to prevent hostile use of GPS and its augmentations without unduly disrupting or degrading civilian uses."

Timeline and modernization

Summary of satellites[15]
Block Launch
Period		 Satellite launches Currently in orbit
and healthy
Suc-
cess		 Fail-
ure		 In prep-
aration		 Plan-
ned
I 1978–1985 10 1 0 0 0
II 1989–1990 9 0 0 0 0
IIA 1990–1997 19 0 0 0 10
IIR 1997–2004 12 1 0 0 12
IIR-M 2005–2009 8 0 0 0 7
IIF 2010– 2 0 10 0 2
IIIA 2014– 0 0 0 12 0
IIIB Theoretical 0 0 0 8 0
IIIC Theoretical 0 0 0 16 0
Total 60 2 10 36 31
(Last update: 24 May 2010)

PRN 01 from Block IIR-M is unhealthy
PRN 25 from Block IIA is unhealthy
PRN 32 from Block IIA is unhealthy
[16] For a more complete list, see list of GPS satellite launches

Awards

On February 10, 1993, the National Aeronautic Association selected the GPS Team as winners of the 1992 Robert J. Collier Trophy, the nation's most prestigious aviation award. This team combines researchers from the Naval Research Laboratory, the USAF, the Aerospace Corporation, Rockwell International Corporation, and IBM Federal Systems Company. The citation honors them "for the most significant development for safe and efficient navigation and surveillance of air and spacecraft since the introduction of radio navigation 50 years ago."

Two GPS developers received the National Academy of Engineering Charles Stark Draper Prize for 2003:

In 1998, GPS technology was inducted into the Space Foundation Space Technology Hall of Fame.[35]

Francis X. Kane (Col. USAF, ret.) was inducted into the U.S. Air Force Space and Missile Pioneers Hall of Fame at Lackland A.F.B., San Antonio, Texas, March 2, 2010 for his role in space technology development and the engineering design concept of GPS conducted as part of Project 621B.

On October 4, 2011, the International Astronautical Federation (IAF) awarded the Global Positioning System (GPS) its 60th Anniversary Award, nominated by IAF member, the American Institute for Aeronautics and Astronautics (AIAA). The IAF Honors and Awards Committee recognized the uniqueness of the GPS program and the exemplary role it has played in building international collaboration for the benefit of humanity.

Basic concept of GPS

A GPS receiver calculates its position by precisely timing the signals sent by GPS satellites high above the Earth. Each satellite continually transmits messages that include

The receiver uses the messages it receives to determine the transit time of each message and computes the distance to each satellite. These distances along with the satellites' locations are used with the possible aid of trilateration, depending on which algorithm is used, to compute the position of the receiver. This position is then displayed, perhaps with a moving map display or latitude and longitude; elevation information may be included. Many GPS units show derived information such as direction and speed, calculated from position changes.

Three satellites might seem enough to solve for position since space has three dimensions and a position near the Earth's surface can be assumed. However, even a very small clock error multiplied by the very large speed of light[36] — the speed at which satellite signals propagate — results in a large positional error. Therefore receivers use four or more satellites to solve for both the receiver's location and time. The very accurately computed time is effectively hidden by most GPS applications, which use only the location. A few specialized GPS applications do however use the time; these include time transfer, traffic signal timing, and synchronization of cell phone base stations.

Although four satellites are required for normal operation, fewer apply in special cases. If one variable is already known, a receiver can determine its position using only three satellites. For example, a ship or aircraft may have known elevation. Some GPS receivers may use additional clues or assumptions (such as reusing the last known altitude, dead reckoning, inertial navigation, or including information from the vehicle computer) to give a less accurate (degraded) position when fewer than four satellites are visible.[37][38][39]

Position calculation introduction

To provide an introductory description of how a GPS receiver works, error effects are deferred to a later section. Using messages received from a minimum of four visible satellites, a GPS receiver is able to determine the times sent and then the satellite positions corresponding to these times sent. The x, y, and z components of position, and the time sent, are designated as \scriptstyle\left[x_i,\, y_i,\, z_i,\, t_i\right] where the subscript i is the satellite number and has the value 1, 2, 3, or 4. 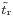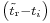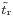Knowing the indicated time the message was received \scriptstyle\ \tilde{t}_\text{r}, the GPS receiver could compute the transit time of the message as \scriptstyle\left ( \tilde{t}_\text{r}-t_i\right ) , if \scriptstyle\ \tilde{t}_\text{r} would be equal to correct reception time, 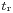\scriptstyle\ t_\text{r}. A pseudorange, 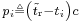\scriptstyle p_i \triangleq \left ( \tilde{t}_\text{r}-t_i\right )c, would be the traveling distance of the message, assuming it traveled at the speed of light, c.

A satellite's position and pseudorange define a sphere, centered on the satellite, with radius equal to the pseudorange. The position of the receiver is somewhere on the surface of this sphere. Thus with four satellites, the indicated position of the GPS receiver is at or near the intersection of the surfaces of four spheres. In the ideal case of no errors, the GPS receiver would be at a precise intersection of the four surfaces.

If the surfaces of two spheres intersect at more than one point, they intersect in a circle. The article trilateration shows this mathematically. A figure, Two Sphere Surfaces Intersecting in a Circle, is shown below. Two points where the surfaces of the spheres intersect are clearly shown in the figure. The distance between these two points is the diameter of the circle of intersection. The intersection of a third spherical surface with the first two will be its intersection with that circle; in most cases of practical interest, this means they intersect at two points.[40] Another figure, Surface of Sphere Intersecting a Circle (not a solid disk) at Two Points, illustrates the intersection. The two intersections are marked with dots. Again the article trilateration clearly shows this mathematically.

For automobiles and other near-earth vehicles, the correct position of the GPS receiver is the intersection closest to the Earth's surface.[41] For space vehicles, the intersection farthest from Earth may be the correct one.

The correct position for the GPS receiver is also the intersection closest to the surface of the sphere corresponding to the fourth satellite.

Correcting a GPS receiver's clock

One of the most significant error sources is the GPS receiver's clock. Because of the very large value of the speed of light, c, the estimated distances from the GPS receiver to the satellites, the pseudoranges, are very sensitive to errors in the GPS receiver clock; for example an error of one microsecond (0.000 001 second) corresponds to an error of 300 metres (980 ft). This suggests that an extremely accurate and expensive clock is required for the GPS receiver to work. Because manufacturers prefer to build inexpensive GPS receivers for mass markets, the solution for this dilemma is based on the way sphere surfaces intersect in the GPS problem.

It is likely that the surfaces of the three spheres intersect, because the circle of intersection of the first two spheres is normally quite large, and thus the third sphere surface is likely to intersect this large circle. It is very unlikely that the surface of the sphere corresponding to the fourth satellite will intersect either of the two points of intersection of the first three, because any clock error could cause it to miss intersecting a point. However, the distance from the valid estimate of GPS receiver position to the surface of the sphere corresponding to the fourth satellite can be used to compute a clock correction.

Let 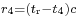\scriptstyle r_4 = \left ( t_\text{r}-t_4\right )c, which is the distance from the valid estimate of GPS receiver position to the fourth satellite, and let 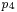\scriptstyle p_4 denote the pseudorange of the fourth satellite. Let 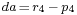\scriptstyle da \,=\, r_4 \,-\, p_4, which is the distance from the computed GPS receiver position to the surface of the sphere corresponding to the fourth satellite. Thus the quotient, 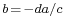\scriptstyle b \,=\, - da / c\ , provides an estimate of GPS receiver's clock bias: 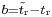\scriptstyle b= \tilde{t}_\text{r} - t_\text{r}, where 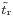\scriptstyle\ \tilde{t}_\text{r} is the time indicated by the receiver's on-board clock and 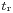\scriptstyle\ t_\text{r} is the correct reception time. The GPS receiver clock can be advanced if 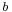\scriptstyle b is positive or delayed if 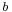\scriptstyle b is negative.

Structure

The current GPS consists of three major segments. These are the space segment (SS), a control segment (CS), and a user segment (US).[42] The U.S. Air Force develops, maintains, and operates the space and control segments. GPS satellites broadcast signals from space, and each GPS receiver uses these signals to calculate its three-dimensional location (latitude, longitude, and altitude) and the current time.[43]

The space segment is composed of 24 to 32 satellites in medium Earth orbit and also includes the payload adapters to the boosters required to launch them into orbit. The control segment is composed of a master control station, an alternate master control station, and a host of dedicated and shared ground antennas and monitor stations. The user segment is composed of hundreds of thousands of U.S. and allied military users of the secure GPS Precise Positioning Service, and tens of millions of civil, commercial, and scientific users of the Standard Positioning Service (see GPS navigation devices).

Space segment

See also: GPS satellite and List of GPS satellite launches

The space segment (SS) is composed of the orbiting GPS satellites, or Space Vehicles (SV) in GPS parlance. The GPS design originally called for 24 SVs, eight each in three approximately circular orbits,[44] but this was modified to six orbital planes with four satellites each.[45] The orbits are centered on the Earth, not rotating with the Earth, but instead fixed with respect to the distant stars.[46] The six orbit planes have approximately 55° inclination (tilt relative to Earth's equator) and are separated by 60° right ascension of the ascending node (angle along the equator from a reference point to the orbit's intersection).[47] The orbital period is one-half a sidereal day, i.e. 11 hours and 58 minutes.[48] The orbits are arranged so that at least six satellites are always within line of sight from almost everywhere on Earth's surface.[49] The result of this objective is that the four satellites are not evenly spaced (90 degrees) apart within each orbit. In general terms, the angular difference between satellites in each orbit is 30, 105, 120, and 105 degrees apart which, of course, sum to 360 degrees.

Orbiting at an altitude of approximately 20,200 km (12,600 mi); orbital radius of approximately 26,600 km (16,500 mi), each SV makes two complete orbits each sidereal day, repeating the same ground track each day.[50] This was very helpful during development because even with only four satellites, correct alignment means all four are visible from one spot for a few hours each day. For military operations, the ground track repeat can be used to ensure good coverage in combat zones.

As of March 2008,[51] there are 31 actively broadcasting satellites in the GPS constellation, and two older, retired from active service satellites kept in the constellation as orbital spares. The additional satellites improve the precision of GPS receiver calculations by providing redundant measurements. With the increased number of satellites, the constellation was changed to a nonuniform arrangement. Such an arrangement was shown to improve reliability and availability of the system, relative to a uniform system, when multiple satellites fail.[52] About nine satellites are visible from any point on the ground at any one time (see animation at right), ensuring considerable redundancy over the minimum four satellites needed for a position.

Control segment

The control segment is composed of

  1. a master control station (MCS),
  2. an alternate master control station,
  3. four dedicated ground antennas and
  4. six dedicated monitor stations

The MCS can also access U.S. Air Force Satellite Control Network (AFSCN) ground antennas (for additional command and control capability) and NGA (National Geospatial-Intelligence Agency) monitor stations. The flight paths of the satellites are tracked by dedicated U.S. Air Force monitoring stations in Hawaii, Kwajalein, Ascension Island, Diego Garcia, Colorado Springs, Colorado and Cape Canaveral, along with shared NGA monitor stations operated in England, Argentina, Ecuador, Bahrain, Australia and Washington DC.[53] The tracking information is sent to the Air Force Space Command's MCS at Schriever Air Force Base 25 km (16 mi) ESE of Colorado Springs, which is operated by the 2nd Space Operations Squadron (2 SOPS) of the U.S. Air Force. Then 2 SOPS contacts each GPS satellite regularly with a navigational update using dedicated or shared (AFSCN) ground antennas (GPS dedicated ground antennas are located at Kwajalein, Ascension Island, Diego Garcia, and Cape Canaveral). These updates synchronize the atomic clocks on board the satellites to within a few nanoseconds of each other, and adjust the ephemeris of each satellite's internal orbital model. The updates are created by a Kalman filter that uses inputs from the ground monitoring stations, space weather information, and various other inputs.[54]

Satellite maneuvers are not precise by GPS standards. So to change the orbit of a satellite, the satellite must be marked unhealthy, so receivers will not use it in their calculation. Then the maneuver can be carried out, and the resulting orbit tracked from the ground. Then the new ephemeris is uploaded and the satellite marked healthy again.

The Operation Control Segment (OCS) currently serves as the control segment of record. It provides the operational capability that supports global GPS users and keeps the GPS system operational and performing within specification.

OCS successfully replaced the legacy 1970’s-era mainframe computer at Schriever Air Force Base in September 2007. After installation, the system helped enable upgrades and provide a foundation for a new security architecture that supported the U.S. armed forces. OCS will continue to be the ground control system of record until the new segment, Next Generation GPS Operation Control System [2] (OCX), is fully developed and functional.

The new capabilities provided by OCX will be the cornerstone for revolutionizing GPS’s mission capabilities, and enabling [55] Air Force Space Command to greatly enhance GPS operational services to U.S. combat forces, civil partners and myriad of domestic and international users.

The GPS OCX program also will reduce cost, schedule and technical risk. It is designed to provide 50% [56] sustainment cost savings through efficient software architecture and Performance-Based Logistics. In addition, GPS OCX expected to cost millions less than the cost to upgrade OCS while providing four times the capability.

The GPS OCX program represents a critical part of GPS modernization and provides significant information assurance improvements over the current GPS OCS program.

On September 14, 2011,[57] the U.S. Air Force announced the completion of GPS OCX Preliminary Design Review and confirmed that the OCX program is ready for the next phase of development.

The GPS OCX program has achieved major milestones and is on track to support the GPS IIIA launch in May 2014.

User segment

The user segment is composed of hundreds of thousands of U.S. and allied military users of the secure GPS Precise Positioning Service, and tens of millions of civil, commercial and scientific users of the Standard Positioning Service. In general, GPS receivers are composed of an antenna, tuned to the frequencies transmitted by the satellites, receiver-processors, and a highly stable clock (often a crystal oscillator). They may also include a display for providing location and speed information to the user. A receiver is often described by its number of channels: this signifies how many satellites it can monitor simultaneously. Originally limited to four or five, this has progressively increased over the years so that, as of 2007, receivers typically have between 12 and 20 channels.[58]

GPS receivers may include an input for differential corrections, using the RTCM SC-104 format. This is typically in the form of an RS-232 port at 4,800 bit/s speed. Data is actually sent at a much lower rate, which limits the accuracy of the signal sent using RTCM . Receivers with internal DGPS receivers can outperform those using external RTCM data . As of 2006, even low-cost units commonly include Wide Area Augmentation System (WAAS) receivers.

Many GPS receivers can relay position data to a PC or other device using the NMEA 0183 protocol. Although this protocol is officially defined by the National Marine Electronics Association (NMEA),[59] references to this protocol have been compiled from public records, allowing open source tools like gpsd to read the protocol without violating intellectual property laws. Other proprietary protocols exist as well, such as the SiRF and MTK protocols. Receivers can interface with other devices using methods including a serial connection, USB, or Bluetooth.

Further information: GPS navigation device

Applications

While originally a military project, GPS is considered a dual-use technology, meaning it has significant military and civilian applications.

GPS has become a widely deployed and useful tool for commerce, scientific uses, tracking, and surveillance. GPS's accurate time facilitates everyday activities such as banking, mobile phone operations, and even the control of power grids by allowing well synchronized hand-off switching.[43]

Civilian

See also: GNSS applications and GPS navigation device

Many civilian applications use one or more of GPS's three basic components: absolute location, relative movement, and time transfer.

Restrictions on civilian use

The U.S. Government controls the export of some civilian receivers. All GPS receivers capable of functioning above 18 kilometres (11 mi) altitude and 515 metres per second (1,001 kn)[62] are classified as munitions (weapons) for which State Department export licenses are required. These limits attempt to prevent use of a receiver in a ballistic missile. They would not prevent use in a cruise missile because their altitudes and speeds are similar to those of ordinary aircraft.

This rule applies even to otherwise purely civilian units that only receive the L1 frequency and the C/A (Coarse/Acquisition) code and cannot correct for Selective Availability (SA), etc.

Disabling operation above these limits exempts the receiver from classification as a munition. Vendor interpretations differ. The rule targets operation given the combination of altitude and speed, while some receivers stop operating even when stationary. This has caused problems with some amateur radio balloon launches that regularly reach 30 kilometres (19 mi).

These limits only apply to units exported from (or which have components exported from) the USA - there is a growing trade in various components, including GPS units, supplied by other countries, which are expressly sold as ITAR-free.

Military

As of 2009, military applications of GPS include:

Communication

Main article: GPS signals

The navigational signals transmitted by GPS satellites encode a variety of information including satellite positions, the state of the internal clocks, and the health of the network. These signals are transmitted on two separate carrier frequencies that are common to all satellites in the network. Two different encodings are used: a public encoding that enables lower resolution navigation, and an encrypted encoding used by the U.S. military.

Message format

GPS message format
Subframes Description
1 Satellite clock,
GPS time relationship
2–3 Ephemeris
(precise satellite orbit)
4–5 Almanac component
(satellite network synopsis,
error correction)

Each GPS satellite continuously broadcasts a navigation message on L1 C/A and L2 P/Y at a rate of 50 bits per second (see bitrate). Each complete message takes 750 seconds (12 1/2 minutes) to complete. The message structure has a basic format of a 1500-bit-long frame made up of five subframes, each subframe being 300 bits (6 seconds) long. Subframes 4 and 5 are subcommutated 25 times each, so that a complete data message requires the transmission of 25 full frames. Each subframe consists of ten words, each 30 bits long. Thus, with 300 bits in a subframe x 5 subframes in a frame x 25 frames in a message, each message is 37,500 bits long. At a transmission rate of 50 bps, this gives 750 seconds to transmit an entire almanac message. Each 30-second frame begins precisely on the minute or half minute as indicated by the atomic clock on each satellite.[70]

The first part of the message encodes the week number and the time within the week,[71] as well as the data about the health of the satellite. The second part of the message, the ephemeris, provides the precise orbit for the satellite. The last part of the message, the almanacsub commutated in subframes 4 & 5, contains coarse orbit and status information for up to 32 satellites in the constellation as well as data related to error correction. Thus, in order to obtain an accurate satellite location from this transmitted message the reciver must demodulate the message from each satellite it includes in its solution for 18 to 30 seconds. In order to collect all the transmitted almanacs the reciver must demodulate the message for 732 to 750 seconds or 12 1/2 minutes.[72]

All satellites broadcast at the same frequencies. Signals are encoded using code division multiple access (CDMA) allowing messages from individual satellites to be distinguished from each other based on unique encodings for each satellite (that the receiver must be aware of). Two distinct types of CDMA encodings are used: the coarse/acquisition (C/A) code, which is accessible by the general public, and the precise (P) code, that is encrypted so that only the U.S. military can access it.

The ephemeris is updated every 2 hours and is generally valid for 4 hours, with provisions for updates every 6 hours or longer in non-nominal conditions. The almanac is updated typically every 24 hours. Additionally data for a few weeks following is uploaded in case of transmission updates that delay data upload.

Satellite frequencies

GPS frequency overview
Band Frequency Description
L1 1575.42 MHz Coarse-acquisition (C/A) and encrypted precision P(Y) codes, plus the L1 civilian (L1C) and military (M) codes on future Block III satellites.
L2 1227.60 MHz P(Y) code, plus the L2C and military codes on the Block IIR-M and newer satellites.
L3 1381.05 MHz Used for nuclear detonation (NUDET) detection.
L4 1379.913 MHz Being studied for additional ionospheric correction.
L5 1176.45 MHz Proposed for use as a civilian safety-of-life (SoL) signal.

All satellites broadcast at the same two frequencies, 1.57542 GHz (L1 signal) and 1.2276 GHz (L2 signal). The satellite network uses a CDMA spread-spectrum technique where the low-bitrate message data is encoded with a high-rate pseudo-random (PRN) sequence that is different for each satellite. The receiver must be aware of the PRN codes for each satellite to reconstruct the actual message data. The C/A code, for civilian use, transmits data at 1.023 million chips per second, whereas the P code, for U.S. military use, transmits at 10.23 million chips per second. The L1 carrier is modulated by both the C/A and P codes, while the L2 carrier is only modulated by the P code.[73] The P code can be encrypted as a so-called P(Y) code that is only available to military equipment with a proper decryption key. Both the C/A and P(Y) codes impart the precise time-of-day to the user.

The L3 signal at a frequency of 1.38105 GHz is used by the United States Nuclear Detonation (NUDET) Detection System (USNDS) to detect, locate, and report nuclear detonations (NUDETs) in the Earth's atmosphere and near space.[74] One usage is the enforcement of nuclear test ban treaties.

The L4 band at 1.379913 GHz is being studied for additional ionospheric correction.

The L5 frequency band at 1.17645 GHZ was added in the process of GPS modernization. This frequency falls into an internationally protected range for aeronautical navigation, promising little or no interference under all circumstances. The first Block IIF satellite that would provide this signal is set to be launched in 2009.[75] The L5 consists of two carrier components that are in phase quadrature with each other. Each carrier component is bi-phase shift key (BPSK) modulated by a separate bit train. "L5, the third civil GPS signal, will eventually support safety-of-life applications for aviation and provide improved availability and accuracy." [76]

A conditional waiver has recently been granted to LightSquared to operate a terrestrial broadband service near the L1 band. Although LightSquared had applied for a license to operate in the 1525 to 1559 band as early as 2003 and it was put out for public comment, the FCC asked LightSquared to form a study group with the GPS community to test GPS receivers and identify issue that might arise due to the larger signal power from the LightSquared terrestrial network. The GPS community had not objected to the LightSquared (formerly MSV and SkyTerra) applications until November 2010, when LightSquared applied for a modification to its Ancillary Terrestrial Component (ATC) authorization. This filing (SAT-MOD-20101118-00239) amounted to a request to run several orders of magnitude more power in the same frequency band for terrestrial base stations, essentially repurposing what was supposed to be a "quiet neighborhood" for signals from space as the equivalent of a cellular network. Testing in the first half of 2011 has demonstrated that the impact of the lower 10 MHz of spectrum is minimal to GPS devices (less than 1% of the total GPS devices are affected). The upper 10 MHz intended for use by LightSquared may have some impact on GPS devices. There is some concern that this will seriously degrade the GPS signal for many consumer uses.[77][78] Aviation Week magazine reports that the latest testing (June 2011) confirms "significant jamming" of GPS by LightSquared's system.[79]

Demodulation and decoding

Because all of the satellite signals are modulated onto the same L1 carrier frequency, the signals must be separated after demodulation. This is done by assigning each satellite a unique binary sequence known as a Gold code. The signals are decoded after demodulation using addition of the Gold codes corresponding to the satellites monitored by the receiver.[80][81]

If the almanac information has previously been acquired, the receiver picks the satellites to listen for by their PRNs, unique numbers in the range 1 through 32. If the almanac information is not in memory, the receiver enters a search mode until a lock is obtained on one of the satellites. To obtain a lock, it is necessary that there be an unobstructed line of sight from the receiver to the satellite. The receiver can then acquire the almanac and determine the satellites it should listen for. As it detects each satellite's signal, it identifies it by its distinct C/A code pattern. There can be a delay of up to 30 seconds before the first estimate of position because of the need to read the ephemeris data.

Processing of the navigation message enables the determination of the time of transmission and the satellite position at this time. For more information see Demodulation and Decoding, Advanced.

Navigation equations

The receiver uses messages received from satellites to determine the satellite positions and time sent. The x, y, and z components of satellite position and the time sent are designated as [xi, yi, zi, ti] where the subscript i denotes the satellite and has the value 1, 2, ..., n, where 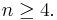n \ge 4. Knowing when the message was received 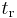\, t_\text{r}, the receiver computes the message's transit time as \, t_\text{r}- t_i. 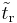Note that the receiver indeed knows the reception time indicated by its on-board clock, \, \tilde{t}_\text{r} rather than 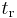\, t_\text{r}. Assuming the message traveled at the speed of light (c) the distance traveled is (tr − ti)c. Knowing the distance from receiver to satellite and the satellite's position implies that the receiver is on the surface of a sphere centered at the satellite's position. Thus the receiver is at or near the intersection of the surfaces of the spheres. In the ideal case of no errors, the receiver is at the intersection of the surfaces of the spheres.

Let b denote the clock error or bias, the amount that the receiver's clock is off. The receiver has four unknowns, the three components of GPS receiver position and the clock bias [x, y, z, b]. The equations of the sphere surfaces are given by:

(x-x_i)^2 %2B (y-y_i)^2 %2B (z-z_i)^2 = \bigl([ t_\text{r} %2B b - t_i]c\bigr)^2, \; i=1,2,\dots,n

or in terms of pseudoranges, 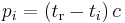p_i = \left ( t_\text{r} - t_i \right )c, as

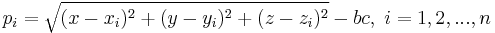p_i = \sqrt{(x-x_i)^2 %2B (y-y_i)^2 %2B (z-z_i)^2}- bc, \;i=1,2,...,n .

These equations can be solved by algebraic or numerical methods.

Bancroft's method

Bancroft's method involves an algebraic as opposed to numerical method and can be used for the case of four satellites or for the case of more than four satellites.[82][83] If there are four satellites then Bancroft's method provides the unique solution for the four unknowns. If there are more than four satellites then Bancroft's method provides the solution which minimizes the sum of the squares of the errors for the over determined system.

Trilateration

The receiver can use trilateration [84][85] and one dimensional numerical root finding.[86] Trilateration is used to determine the position based on three satellite's pseudoranges. In the usual case of two intersections, the point nearest the surface of the sphere corresponding to the fourth satellite is chosen. Let d denote the signed distance from the receiver position to the sphere around the fourth satellite. The notation, d(correction) shows this as a function of the correction, because it changes the pseudoranges. The problem is to determine the correction such that d(correction) = 0. This is the familiar problem of finding the zeroes of a one dimensional non-linear function of a scalar variable. Iterative numerical methods, such as those found in the chapter on root finding in Numerical Recipes can solve this type of problem.[86]

Multidimensional Newton-Raphson calculations

Alternatively, multidimensional root finding method such as Newton-Raphson method can be used.[86] The approach is to linearize around an approximate solution, say \ \left [x^{(k)}, y ^{(k)}, z^{(k)}, b^{(k)}\right ] from iteration k, then solve the linear equations derived from the quadratic equations above to obtain \left [x^{(k%2B1)}, y^{(k%2B1)}, z^{(k%2B1)}, b^{(k%2B1)}\right ]. Although there is no guarantee that the method always converges due to the fact that multidimensional roots cannot be bounded, when a neighborhood containing a solution is known as is usually the case for GPS, it is quite likely that a solution will be found.[86] It has been shown[87] that results are comparable in accuracy to those of the Bancroft's method.

Additional methods for more than four satellites

When more than four satellites are available, the calculation can use the four best or more than four, considering number of channels, processing capability, and geometric dilution of precision (GDOP). Using more than four is an over-determined system of equations with no unique solution, which must be solved by least-squares or a similar technique.[83] If all visible satellites are used, the results are as good as or better than using the four best. Errors can be estimated through the residuals. With each combination of four or more satellites, a GDOP factor can be calculated, based on the relative sky directions of the satellites used.[88] As more satellites are picked up, pseudoranges from various 4-way combinations can be processed to add more estimates to the location and clock offset. The receiver then takes the weighted average of these positions and clock offsets. After the final location and time are calculated, the location is expressed in a specific coordinate system such as latitude and longitude, using the WGS 84 geodetic datum or a country-specific system.[89]

Error sources and analysis

Error analysis for the Global Positioning System is an important aspect for determining what errors and their magnitude are to be expected. GPS errors are affected by geometric dilution of precision and depend on signal arrival time errors, numerical errors, atmospherics effects, ephemeris errors, multipath errors and other effects. The single largest source of error in modelling the orbital dynamics is due to variability in solar radiation pressure [90].

Accuracy enhancement and surveying

Main article: GPS augmentation

Augmentation

Integrating external information into the calculation process can materially improve accuracy. Such augmentation systems are generally named or described based on how the information arrives. Some systems transmit additional error information (such as clock drift, ephemera, or ionospheric delay), others characterize prior errors, while a third group provides additional navigational or vehicle information.

Examples of augmentation systems include the Wide Area Augmentation System (WAAS), European Geostationary Navigation Overlay Service (EGNOS), Differential GPS, Inertial Navigation Systems (INS) and Assisted GPS.

Precise monitoring

Accuracy can be improved through precise monitoring and measurement of existing GPS signals in additional or alternate ways.

The largest remaining error is usually the unpredictable delay through the ionosphere. The spacecraft broadcast ionospheric model parameters, but errors remain. This is one reason GPS spacecraft transmit on at least two frequencies, L1 and L2. Ionospheric delay is a well-defined function of frequency and the total electron content (TEC) along the path, so measuring the arrival time difference between the frequencies determines TEC and thus the precise ionospheric delay at each frequency.

Military receivers can decode the P(Y)-code transmitted on both L1 and L2. Without decryption keys, it is still possible to use a codeless technique to compare the P(Y) codes on L1 and L2 to gain much of the same error information. However, this technique is slow, so it is currently available only on specialized surveying equipment. In the future, additional civilian codes are expected to be transmitted on the L2 and L5 frequencies (see GPS modernization). Then all users will be able to perform dual-frequency measurements and directly compute ionospheric delay errors.

A second form of precise monitoring is called Carrier-Phase Enhancement (CPGPS). This corrects the error that arises because the pulse transition of the PRN is not instantaneous, and thus the correlation (satellite-receiver sequence matching) operation is imperfect. CPGPS uses the L1 carrier wave, which has a period of 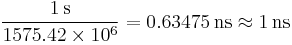\frac{1\,\mathrm{s}}{1575.42 \times 10^6} = 0.63475\,\mathrm{ns} \approx 1\, \mathrm{ns} \ , which is about one-thousandth of the C/A Gold code bit period of 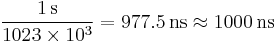\frac{1\, \mathrm{s}}{1023 \times 10^3} = 977.5 \, \mathrm{ns} \approx 1000 \, \mathrm{ns} \ , to act as an additional clock signal and resolve the uncertainty. The phase difference error in the normal GPS amounts to 2–3 metres (6.6–9.8 ft) of ambiguity. CPGPS working to within 1% of perfect transition reduces this error to 3 centimetres (1.2 in) of ambiguity. By eliminating this error source, CPGPS coupled with DGPS normally realizes between 20–30 centimetres (7.9–12 in) of absolute accuracy.

Relative Kinematic Positioning (RKP) is a third alternative for a precise GPS-based positioning system. In this approach, determination of range signal can be resolved to a precision of less than 10 centimetres (3.9 in). This is done by resolving the number of cycles that the signal is transmitted and received by the receiver by using a combination of differential GPS (DGPS) correction data, transmitting GPS signal phase information and ambiguity resolution techniques via statistical tests—possibly with processing in real-time (real-time kinematic positioning, RTK).

Timekeeping

Timekeeping and leap seconds

While most clocks are synchronized to Coordinated Universal Time (UTC), the atomic clocks on the satellites are set to GPS time (GPST; see the page of United States Naval Observatory). The difference is that GPS time is not corrected to match the rotation of the Earth, so it does not contain leap seconds or other corrections that are periodically added to UTC. GPS time was set to match Coordinated Universal Time (UTC) in 1980, but has since diverged. The lack of corrections means that GPS time remains at a constant offset with International Atomic Time (TAI) (TAI – GPS = 19 seconds). Periodic corrections are performed on the on-board clocks to keep them synchronized with ground clocks.[91]

The GPS navigation message includes the difference between GPS time and UTC, which as of 2011 is 15 seconds because of the leap second added to UTC December 31, 2008. Receivers add this offset to GPS time to calculate UTC and specific timezone values. New GPS units may not show the correct UTC time until after receiving the UTC offset message. The GPS-UTC offset field can accommodate 255 leap seconds (eight bits) that, given the current period of the Earth's rotation (with one leap second introduced approximately every 18 months), should be sufficient to last until approximately the year 2300.

Timekeeping accuracy

GPS time is accurate to about 14 nanoseconds.[92]

Timekeeping format

As opposed to the year, month, and day format of the Gregorian calendar, the GPS date is expressed as a week number and a seconds-into-week number. The week number is transmitted as a ten-bit field in the C/A and P(Y) navigation messages, and so it becomes zero again every 1,024 weeks (19.6 years). GPS week zero started at 00:00:00 UTC (00:00:19 TAI) on January 6, 1980, and the week number became zero again for the first time at 23:59:47 UTC on August 21, 1999 (00:00:19 TAI on August 22, 1999). To determine the current Gregorian date, a GPS receiver must be provided with the approximate date (to within 3,584 days) to correctly translate the GPS date signal. To address this concern the modernized GPS navigation message uses a 13-bit field that only repeats every 8,192 weeks (157 years), thus lasting until the year 2137 (157 years after GPS week zero).

Carrier phase tracking (surveying)

Another method that is used in surveying applications is carrier phase tracking. The period of the carrier frequency multiplied by the speed of light gives the wavelength, which is about 0.19 meters for the L1 carrier. Accuracy within 1% of wavelength in detecting the leading edge reduces this component of pseudorange error to as little as 2 millimeters. This compares to 3 meters for the C/A code and 0.3 meters for the P code.

However, 2 millimeter accuracy requires measuring the total phase—the number of waves multiplied by the wavelength plus the fractional wavelength, which requires specially equipped receivers. This method has many surveying applications.

Triple differencing followed by numerical root finding, and a mathematical technique called least squares can estimate the position of one receiver given the position of another. First, compute the difference between satellites, then between receivers, and finally between epochs. Other orders of taking differences are equally valid. Detailed discussion of the errors is omitted.

The satellite carrier total phase can be measured with ambiguity as to the number of cycles. Let 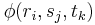\ \phi(r_i, s_j, t_k) denote the phase of the carrier of satellite j measured by receiver i at time 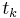\ \ t_k . This notation shows the meaning of the subscripts i, j, and k. 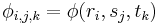The receiver (r), satellite (s), and time (t) come in alphabetical order as arguments of \ \phi and to balance readability and conciseness, let \ \phi_{i,j,k} = \phi(r_i, s_j, t_k) be a concise abbreviation. Also we define three functions, :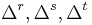\ \Delta^r, \Delta^s, \Delta^t , which return differences between receivers, satellites, and time points, respectively. Each function has variables with three subscripts as its arguments. These three functions are defined below. If 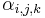\ \alpha_{i,j,k} is a function of the three integer arguments, i, j, and k then it is a valid argument for the functions, :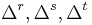\ \Delta^r, \Delta^s, \Delta^t , with the values defined as

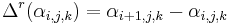\ \Delta^r(\alpha_{i,j,k}) = \alpha_{i%2B1,j,k} - \alpha_{i,j,k} ,
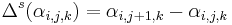\ \Delta^s(\alpha_{i,j,k}) = \alpha_{i,j%2B1,k} - \alpha_{i,j,k} , and
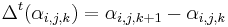\ \Delta^t(\alpha_{i,j,k}) = \alpha_{i,j,k%2B1} - \alpha_{i,j,k}  .

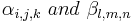Also if \ \alpha_{i,j,k}\ and\ \beta_{l,m,n} are valid arguments for the three functions and a and b are constants then 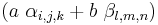\ ( a\ \alpha_{i,j,k} %2B b\ \beta_{l,m,n} ) is a valid argument with values defined as

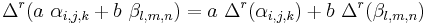\ \Delta^r(a\ \alpha_{i,j,k} %2B b\ \beta_{l,m,n}) = a \ \Delta^r(\alpha_{i,j,k}) %2B b \ \Delta^r(\beta_{l,m,n}),
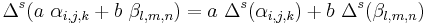\ \Delta^s(a\ \alpha_{i,j,k} %2B b\ \beta_{l,m,n} )= a \ \Delta^s(\alpha_{i,j,k}) %2B b \ \Delta^s(\beta_{l,m,n}), and
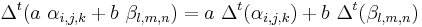\ \Delta^t(a\ \alpha_{i,j,k} %2B b\ \beta_{l,m,n} )= a \ \Delta^t(\alpha_{i,j,k}) %2B b \ \Delta^t(\beta_{l,m,n}) .

Receiver clock errors can be approximately eliminated by differencing the phases measured from satellite 1 with that from satellite 2 at the same epoch.[93] This difference is designated as 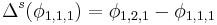\ \Delta^s(\phi_{1,1,1}) = \phi_{1,2,1} - \phi_{1,1,1}

Double differencing[94] computes the difference of receiver 1's satellite difference from that of receiver 2. This approximately eliminates satellite clock errors. This double difference is:

\begin{align} \Delta^r(\Delta^s(\phi_{1,1,1}))\,&=\,\Delta^r(\phi_{1,2,1} - \phi_{1,1,1}) &=\,\Delta^r(\phi_{1,2,1}) - \Delta^r(\phi_{1,1,1}) &=\,(\phi_{2,2,1} - \phi_{1,2,1}) - (\phi_{2,1,1} - \phi_{1,1,1}) \end{align}

Triple differencing[95] subtracts the receiver difference from time 1 from that of time 2. This eliminates the ambiguity associated with the integral number of wave lengths in carrier phase provided this ambiguity does not change with time. Thus the triple difference result eliminates practically all clock bias errors and the integer ambiguity. Atmospheric delay and satellite ephemeris errors have been significantly reduced. This triple difference is:

\ \Delta^t(\Delta^r(\Delta^s(\phi_{1,1,1})))

Triple difference results can be used to estimate unknown variables. For example if the position of receiver 1 is known but the position of receiver 2 unknown, it may be possible to estimate the position of receiver 2 using numerical root finding and least squares. Triple difference results for three independent time pairs quite possibly will be sufficient to solve for receiver 2's three position components. This may require the use of a numerical procedure.[96][97] An approximation of receiver 2's position is required to use such a numerical method. This initial value can probably be provided from the navigation message and the intersection of sphere surfaces. Such a reasonable estimate can be key to successful multidimensional root finding. Iterating from three time pairs and a fairly good initial value produces one observed triple difference result for receiver 2's position. Processing additional time pairs can improve accuracy, overdetermining the answer with multiple solutions. Least squares can estimate an overdetermined system. Least squares determines the position of receiver 2 which best fits the observed triple difference results for receiver 2 positions under the criterion of minimizing the sum of the squares.

Regulatory spectrum issues concerning GPS receivers

In the United States, GPS receivers are regulated under the Federal Communications Commission's (FCC) Part 15 rules. As indicated in the manuals of GPS-enabled devices sold in the United States, as a Part 15 device, it "must accept any interference received, including interference that may cause undesired operation."[98] With respect to GPS devices in particular, the FCC states that GPS receiver manufacturers, "must use receivers that reasonably discriminate against reception of signals outside their allocated spectrum."[99]

The spectrum allocated for GPS L1 use by the FCC is 1559 to 1610 MHz.[100] Since 1996, the FCC has authorized licensed use of the spectrum neighboring the GPS band of 1525 to 1559 MHz to the Virginia company LightSquared. On March 1, 2001, the FCC received an application from LightSquared's predecessor, Motient Services to use their allocated frequencies for an integrated satellite-terrestrial service.[101] In 2002, the U.S. GPS Industry Council came to an out-of-band-emissions (OOBE) agreement with LightSquared to prevent transmissions from LightSquared's ground-based stations from emitting transmissions into the neighboring GPS band of 1559 to 1610 MHz.[102] In 2004, the FCC adopted the OOBE agreement in its authorization for LightSquared to deploy a ground-based network that used its allocated frequencies of 1525 to 1559 MHz.[103] This authorization was reviewed and approved by the U.S. Interdepartment Radio Advisory Committee, which includes the U.S. Departments of Agriculture, Air Force, Army, Coast Guard, Federal Aviation Administration, National Aeronautics and Space Administration, Interior, and Transportation.[104]

In January 2011, the FCC conditionally authorized LightSquared's wholesale customers, such as Best Buy, Sharp, and C Spire, to be able to only purchase an integrated satellite-ground-based service from LightSquared and re-sell that integrated service on devices that are equipped to only use the ground-based signal using LightSquared's allocated frequencies of 1525 to 1559 MHz.[105] In December 2010, GPS receiver manufacturers expressed concerns to the FCC that LightSquared's signal would interfere with GPS receiver devices[106] although the FCC's policy considerations leading up to the January 2011 order did not pertain to any proposed changes to the maximum number of ground-based LightSquared stations or the maximum power at which these stations could operate. The January 2011 order makes final authorization contingent upon studies of GPS interference issues carried out by a LightSquared led working group along with GPS industry and Federal agency participation.

GPS receiver manufacturers design GPS receivers to use spectrum beyond the GPS-allocated band. In some cases, GPS receivers are designed to use up to 400 MHz of spectrum in either direction of the L1 frequency of 1575.42 MHz.[107] However, as regulated under the FCC's Part 15 rules, GPS receivers are not warranted protection from signals outside GPS-allocated spectrum.[108]

The FCC adopted rules in February 2003 that allowed Mobile Satellite Service (MSS) licensees such as LightSquared to construct ground-based towers in their licensed spectrum to "promote more efficient use of terrestrial wireless spectrum."[109] In July 2010, the FCC stated that it expected LightSquared to use its authority to offer an integrated satellite-terrestrial service to "provide mobile broadband services similar to those provided by terrestrial mobile providers and enhance competition in the mobile broadband sector."[110] However, GPS receiver manufacturers have argued that LightSquared's licensed spectrum of 1525 to 1559 MHz was never envisioned as being used for high-speed wireless broadband although there is no regulatory or legal backing of this claim.[111] To build public support of efforts to reverse the 2004 FCC authorization of LightSquared's network, GPS receiver manufacturer Trimble Navigation Ltd. formed the "Coalition To Save Our GPS."[112]

The FCC and LightSquared have each made public commitments to solve the GPS interference issue before the network is allowed to operate.[113][114] However, according to Chris Dancy of the Aircraft Owners and Pilots Association, airline pilots with the type systems that would be affected "may go off course and not even realize it."[115] The problems could also affect the Federal Aviation Administration upgrade to the air traffic control system, United States Defense Department guidance, and local emergency services including 911.[115]

Other systems

Other satellite navigation systems in use or various states of development include:

See also


References

  1. ^ National Research Council (U.S.). Committee on the Future of the Global Positioning System; National Academy of Public Administration (1995). The global positioning system: a shared national asset : recommendations for technical improvements and enhancements. National Academies Press. p. 16. ISBN 0-309-05283-1. http://books.google.com/books?id=FAHk65slfY4C. , Chapter 1, p. 16
  2. ^ a b "Factsheets : GPS Advanced Control Segment (OCX)". Losangeles.af.mil. 2011-10-25. http://www.losangeles.af.mil/library/factsheets/factsheet.asp?id=18676. Retrieved 2011-11-06. 
  3. ^ Astronautica Acta II, 25 (1956)
  4. ^ "GPS and Relativity". Astronomy.ohio-state.edu. http://www.astronomy.ohio-state.edu/~pogge/Ast162/Unit5/gps.html. Retrieved 2011-11-06. 
  5. ^ Steven Johnson (2010), Where good ideas come from, the natural history of innovation, New York: Riverhead Books 
  6. ^ Jerry Proc. "Omega". Jproc.ca. http://www.jproc.ca/hyperbolic/omega.html. Retrieved 2009-12-08. 
  7. ^ "Why Did the Department of Defense Develop GPS?". Trimble Navigation Ltd. Archived from the original on 2007-10-18. http://web.archive.org/web/20071018151253/http://www.trimble.com/gps/whygps.shtml#0. Retrieved 2010-01-13. 
  8. ^ "Charting a Course Toward Global Navigation". The Aerospace Corporation. http://www.aero.org/publications/crosslink/summer2002/01.html. Retrieved 2010-01-14. 
  9. ^ "A Guide To The Global Positioning System (GPS) — GPS Timeline". Radio Shack. http://support.radioshack.com/support_tutorials/gps/gps_tmline.htm. Retrieved 2010-01-14. 
  10. ^ Michael Russell Rip, James M. Hasik (2002). The Precision Revolution: GPS and the Future of Aerial Warfare. Naval Institute Press. p. 65. ISBN 1557509735. http://books.google.com/?id=mB9W3H90KDUC. Retrieved 2010-01-14. 
  11. ^ "ICAO Completes Fact-Finding Investigation". International Civil Aviation Organization. http://www.icao.int/cgi/goto_m.pl?icao/en/trivia/kal_flight_007.htm. Retrieved 2008-09-15. 
  12. ^ "United States Updates Global Positioning System Technology". America.gov. February 3, 2006. http://www.america.gov/xarchives/display.html?p=washfile-english&y=2006&m=February&x=20060203125928lcnirellep0.5061609. 
  13. ^ "GPS & Selective Availability Q&A". [1]. http://ngs.woc.noaa.gov/FGCS/info/sans_SA/docs/GPS_SA_Event_QAs.pdf. Retrieved 2010-05-28. 
  14. ^ "GPS Modernization Fact Sheet". U.S. Air Force. http://www.pnt.gov/public/docs/2006/modernization.pdf. 
  15. ^ GPS Wing Reaches GPS III IBR Milestone in InsideGNSS November 10, 2008
  16. ^ "GPS almanacs". Navcen.uscg.gov. http://www.navcen.uscg.gov/?pageName=gpsAlmanacs. Retrieved 2010-10-15. 
  17. ^ Dietrich Schroeer, Mirco Elena (2000). Technology Transfer. Ashgate. p. 80. ISBN 075462045X. http://books.google.com/?id=I7JRAAAAMAAJ. Retrieved 2008-05-25. 
  18. ^ Michael Russell Rip, James M. Hasik (2002). The Precision Revolution: GPS and the Future of Aerial Warfare. Naval Institute Press. ISBN 1557509735. http://books.google.com/?id=_wpUAAAAMAAJ. Retrieved 2008-05-25. 
  19. ^ "AF Space Command Chronology". USAF Space Command. http://www.afspc.af.mil/heritage/chronology.asp. Retrieved 20 June 2011. 
  20. ^ "FactSheet: 2nd Space Operations Squadron". USAF Space Command. http://www.schriever.af.mil/library/factsheets/factsheet.asp?id=4045. Retrieved 20 June 2011. 
  21. ^ The Global Positioning System: Assessing National Policies, p.245. RAND corporation
  22. ^ a b "USNO NAVSTAR Global Positioning System". U.S. Naval Observatory. http://tycho.usno.navy.mil/gpsinfo.html. Retrieved 2011-01-07. 
  23. ^ National Archives and Records Administration. U.S. Global Positioning System Policy. March 29, 1996.
  24. ^ "National Executive Committee for Space-Based Positioning, Navigation, and Timing". Pnt.gov. http://pnt.gov/. Retrieved 2010-10-15. 
  25. ^ "Assisted-GPS Test Calls for 3G WCDMA Networks". 3g.co.uk. November 10, 2004. http://www.3g.co.uk/PR/November2004/8641.htm. Retrieved 2010-11-24. 
  26. ^ This story was written by 010907 (2007-09-17). "losangeles.af.mil". losangeles.af.mil. http://www.losangeles.af.mil/news/story.asp?id=123068412. Retrieved 2010-10-15. 
  27. ^ Johnson, Bobbie (May 19, 2009). "GPS system 'close to breakdown'". The Guardian. http://www.guardian.co.uk/technology/2009/may/19/gps-close-to-breakdown. Retrieved 2009-12-08. 
  28. ^ Coursey, David (May 21, 2009). "Air Force Responds to GPS Outage Concerns". ABC News. http://abcnews.go.com/Technology/AheadoftheCurve/story?id=7647002&page=1. Retrieved 2009-05-22. 
  29. ^ "Air Force GPS Problem: Glitch Shows How Much U.S. Military Relies On GPS". Huffingtonpost.comm. http://www.huffingtonpost.com/2010/06/01/air-force-gps-problem-gli_n_595727.html. Retrieved 2010-10-15. 
  30. ^ "Raytheon Awarded Next-Generation Control Segment Contract (OCX)". http://www.gpsworld.com/gnss-system/gps-modernization/news/raytheon-awarded-next-generation-control-segment-contract-ocx-960. Retrieved 2010-02-25. 
  31. ^ "United States Naval Observatory (USNO) GPS Constellation Status". ftp://tycho.usno.navy.mil/pub/gps/gpstd.txt. Retrieved 2009-10-13. 
  32. ^ United States Naval Observatory. GPS Constellation Status. Retrieved December 20, 2008.
  33. ^ "United Launch Alliance GPS IIF-2". United Launch Alliance. http://www.ulalaunch.com/site/pages/News.shtml#/73/. Retrieved 16 July 2011. 
  34. ^ United States Naval Research Laboratory. National Medal of Technology for GPS. November 21, 2005
  35. ^ "Space Technology Hall of Fame, Inducted Technology: Global Positioning System (GPS)". http://www.spacetechhalloffame.org/inductees_1998_Global_Positioning_System.html. 
  36. ^ GPS signals travel at the speed of light, so computing the distance for a given elapsed time is almost a straightforward calculation. However, the speed of light varies slightly between the partial vacuum of space and the atmosphere. A receiver can approximate these effects and produce a reasonable estimate. Once a rough position is determined, some receivers carefully compute the amount of atmosphere the signal traveled through and adjust the distance accordingly.
  37. ^ Georg zur Bonsen, Daniel Ammann, Michael Ammann, Etienne Favey, Pascal Flammant (2005-04-01). "Continuous Navigation Combining GPS with Sensor-Based Dead Reckoning". GPS World. Archived from the original on 2006-11-11. http://web.archive.org/web/20061111202317/http://www.gpsworld.com/gpsworld/article/articleDetail.jsp?id=154870&pageID=6. 
  38. ^ "NAVSTAR GPS User Equipment Introduction" (PDF). United States Government. http://www.navcen.uscg.gov/pubs/gps/gpsuser/gpsuser.pdf.  Chapter 7
  39. ^ "GPS Support Notes" (PDF). January 19, 2007. http://www.navmanwireless.com/uploads/EK/C8/EKC8zb1ITsNwDqWcqLQxiQ/Support_Notes_GPS_OperatingParameters.pdf. Retrieved 2008-11-10. 
  40. ^ It is also possible for a circle and a spherical surface to intersect at zero points, one point, or in the very special case where the centers of the three spheres are co-linear (i.e., all three on the same straight line) the sphere surface could intersect the entire circumference of the circle.
  41. ^ The two intersections are symmetrical about the plane containing the three satellites. Excluding the exceptional case when the three satellites are all in a plane containing the center of the earth, one intersection will be nearer the earth than the other.
  42. ^ John Pike. "GPS III Operational Control Segment (OCX)". Globalsecurity.org. http://www.globalsecurity.org/space/systems/gps_3-ocx.htm. Retrieved 2009-12-08. 
  43. ^ a b "Global Positioning System". Gps.gov. http://www.gps.gov/systems/gps/index.html. Retrieved 2010-06-26. 
  44. ^ Daly, P.. "Navstar GPS and GLONASS: global satellite navigation systems". IEEE. http://ieeexplore.ieee.org/iel1/2219/7072/00285510.pdf?arnumber=285510. 
  45. ^ Dana, Peter H. (1996-08-08). "GPS Orbital Planes" (GIF). http://www.colorado.edu/geography/gcraft/notes/gps/gif/oplanes.gif. 
  46. ^ What the Global Positioning System Tells Us about Relativity. Retrieved January 2, 2007.
  47. ^ GPS Overview from the NAVSTAR Joint Program Office. Retrieved December 15, 2006.
  48. ^ [2] Retrieved October 27, 2011
  49. ^ "USCG Navcen: GPS Frequently Asked Questions". http://www.navcen.uscg.gov/?pageName=gpsFaq. Retrieved 2007-01-31. 
  50. ^ Agnew, D.C. and Larson, K.M. (2007). "Finding the repeat times of the GPS constellation". GPS Solutions (Springer) 11 (1): 71–76. doi:10.1007/s10291-006-0038-4.  This article from author's web site, with minor correction.
  51. ^ Tis-pf-nisws. "Nanu 2008030". http://cgls.uscg.mil/pipermail/gps/2008-March/001625.html. 
  52. ^ Massatt, Paul; Wayne Brady (Summer 2002). "Optimizing performance through constellation management". Crosslink: 17–21. http://www.aero.org/publications/crosslink/summer2002/index.html. 
  53. ^ United States Coast Guard General GPS News 9–9–05
  54. ^ USNO NAVSTAR Global Positioning System. Retrieved May 14, 2006.
  55. ^ "GPS III Operational Control Segment (OCX)". GlobalSecurity.org. http://www.globalsecurity.org/space/systems/gps_3-ocx.htm. 
  56. ^ "The USA’s GPS-III Satellites". Defense Industry Daily. 2011-10-13. http://www.defenseindustrydaily.com/The-USAs-GPS-III-Satellites-04900/. 
  57. ^ "GPS Completes Next Generation Operational Control System PDR". Air Force Space Command News Service. 2011-09-14. http://www.comspacewatch.com/news/viewpr.html?pid=34625. 
  58. ^ Though there are many receiver manufacturers, they almost all use one of the chipsets produced for this purpose. An example: "GPS Receiver Chip Performance Survey". GPS Technology Reviews. http://gpstekreviews.com/2007/04/14/gps-receiver-chip-performance-survey/. 
  59. ^ "Publications and Standards from the National Marine Electronics Association (NMEA)". National Marine Electronics Association. http://www.nmea.org/pub/index.html. Retrieved 2008-06-27. 
  60. ^ "Common View GPS Time Transfer". nist.gov. http://tf.nist.gov/time/commonviewgps.htm. Retrieved 2011-Jul-23. 
  61. ^ "Spotlight GPS pet locator". Spotlightgps.com. http://www.spotlightgps.com/. Retrieved 2010-10-15. 
  62. ^ Arms Control Association.Missile Technology Control Regime. Retrieved May 17, 2006.
  63. ^ "Commanders Digital Assistant explanation and photo". Web.archive.org. 2007-12-01. Archived from the original on 2007-12-01. http://web.archive.org/web/20071201034857/http://peosoldier.army.mil/factsheets/SWAR_LW_DBCS.pdf. Retrieved 2011-11-06. 
  64. ^ "Latest version Commanders Digital Assistant" (PDF). http://peosoldier.army.mil/factsheets/SWAR_LW_CDA.pdf. Retrieved 2009-10-13. 
  65. ^ "Soldier Digital Assistant explanation and photo". Web.archive.org. 2008-06-10. Archived from the original on 2008-06-10. http://web.archive.org/web/20080610092154/http://www.army-technology.com/contractors/computers/lago/lago6.html. Retrieved 2011-11-06. 
  66. ^ Sinha, Vandana (2003-07-24). "Commanders and Soldiers' GPS-receivers". Gcn.com. http://gcn.com/articles/2003/07/24/soldiers-take-digital-assistants-to-war.aspx. Retrieved 2009-10-13. 
  67. ^ "XM982 Excalibur Precision Guided Extended Range Artillery Projectile". GlobalSecurity.org. 2007-05-29. http://www.globalsecurity.org/military/systems/munitions/m982-155.htm. Retrieved 2007-09-26. 
  68. ^ Sandia National Laboratory's Nonproliferation programs and arms control technology.
  69. ^ Dr. Dennis D. McCrady. "The GPS Burst Detector W-Sensor". Sandia National Laboratories. http://www.osti.gov/bridge/servlets/purl/10176800-S2tU7w/native/10176800.pdf. 
  70. ^ "Satellite message format". Gpsinformation.net. http://gpsinformation.net/gpssignal.htm. Retrieved 2010-10-15. 
  71. ^ Michael Woessner, Anja Koehne. "time-of-week". Kowoma.de. http://www.kowoma.de/en/gps/data_composition.htm. Retrieved 2010-10-15. 
  72. ^ "Interface Specification IS-GPS-200, Revision D: Navstar GPS Space Segment/Navigation User Interfaces" (PDF). Navstar GPS Joint Program Office. http://www.losangeles.af.mil/shared/media/document/AFD-070803-059.pdf.  Page 103.
  73. ^ How GPS works. Konowa.de (2005).
  74. ^ TextGenerator Version 2.0. "United States Nuclear Detonation Detection System (USNDS)". Fas.org. http://www.fas.org/spp/military/program/nssrm/initiatives/usnds.htm. Retrieved 2011-11-06. 
  75. ^ First GPS IIF Satellite Undergoes Environmental Testing. GPS World. November 5, 2007.
  76. ^ "Air Force Successfully Transmits an L5 Signal From GPS IIR-20(M) Satellite". LA AFB News Release. http://www.losangeles.af.mil/news/story.asp?storyID=123144001. Retrieved 20 June 2011. 
  77. ^ "Federal Communications Commission Presented Evidence of GPS Signal Interference". GPS World. http://www.gpsworld.com/gnss-system/news/data-shows-disastrous-gps-jamming-fcc-approved-broadcaster-11029?utm_source=GPS&utm_medium=email&utm_campaign=Navigate_01_31_2011&utm_content=data-shows-disastrous-gps-jamming-fcc-approved-broadcaster-11029. Retrieved 2011-11-06. 
  78. ^ "Coalition to Save Our GPS". Saveourgps.org. http://www.saveourgps.org/studies-reports.aspx. Retrieved 2011-11-06. 
  79. ^ "LightSquared Tests Confirm GPS Jamming". Aviation Week. http://www.aviationweek.com/aw/generic/story.jsp?id=news/awx/2011/06/09/awx_06_09_2011_p0-334122.xml&headline=LightSquared%20Tests%20Confirm%20GPS%20Jamming&channel=busav. Retrieved 20 June 2011. 
  80. ^ "GPS Almanacs, NANUS, and Ops Advisories (including archives)". GPS Almanac Information. United States Coast Guard. http://www.navcen.uscg.gov/?pageName=gpsAlmanacs. Retrieved 2009-09-09. 
  81. ^ "George, M., Hamid, M., and Miller A. Gold Code Generators in Virtex DevicesPDF (126 KB)
  82. ^ Bancroft, S. (Jan 1985). "An Algebraic Solution of the GPS Equations". IEEE Transactions on Aerospace and Electronic Systems AES-21: 56–59. doi:10.1109/TAES.1985.310538. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=4104017. 
  83. ^ a b "Global Positioning Systems" (PDF). http://www.macalester.edu/~halverson/math36/GPS.pdf. Retrieved 2010-10-15. 
  84. ^ Position Determination with GPS. Konowa.de (2005).
  85. ^ How GPS Receivers Work at How Stuff Works
  86. ^ a b c d Press, Flannery, Tekolsky, and Vetterling 1986, Numerical Recipes, The Art of Scientific Computing (Cambridge University Press).
  87. ^ "Determination of GPS receiver position using Multivariate Newton-Raphson Technique for over specified cases". http://www.thefreelibrary.com/Determination+of+GPS+receiver+position+using+Multivariate...-a0216041321. 
  88. ^ Dana, Peter H.. "Geometric Dilution of Precision (GDOP) and Visibility". University of Colorado at Boulder. http://www.colorado.edu/geography/gcraft/notes/gps/gps.html#Gdop. Retrieved 2008-07-07. 
  89. ^ Peter H. Dana. "Receiver Position, Velocity, and Time". University of Colorado at Boulder. http://www.colorado.edu/geography/gcraft/notes/gps/gps.html#PosVelTime. Retrieved 2008-07-07. 
  90. ^ IPN Progess Report 42-159 (2004)
  91. ^ "NAVSTAR GPS User Equipment Introduction" (PDF). http://www.navcen.uscg.gov/pubs/gps/gpsuser/gpsuser.pdf.  Section 1.2.2
  92. ^ David W. Allan (1997). "The Science of Timekeeping". Hewlett Packard. http://www.allanstime.com/Publications/DWA/Science_Timekeeping/index.html. 
  93. ^ "Between-Satellite Differencing". Gmat.unsw.edu.au. http://www.gmat.unsw.edu.au/snap/gps/gps_survey/chap6/633.htm. Retrieved 2010-10-15. 
  94. ^ "Double differencing". Gmat.unsw.edu.au. http://www.gmat.unsw.edu.au/snap/gps/gps_survey/chap6/635.htm. Retrieved 2010-10-15. 
  95. ^ "Triple differencing". Gmat.unsw.edu.au. http://www.gmat.unsw.edu.au/snap/gps/gps_survey/chap6/636.htm. Retrieved 2010-10-15. 
  96. ^ chapter on root finding and nonlinear sets of equations
  97. ^ Preview of Root Finding. Books.google.com. 2007. ISBN 9780521880688. http://books.google.com/?id=UQW_VL2H56IC&pg=PA959&lpg=PA959&dq=%22Numerical+Analysis%22+multidimension++root+finding#PPA442,M1. Retrieved 2010-10-15. 
  98. ^ "2011 John Deere StarFire 3000 Operator Manual". John Deere. http://stellarsupport.deere.com/en_US/support/pdf/om/en/ompfp11008_sf3000.pdf. Retrieved 2011-11-13. 
  99. ^ "Federal Communications Commission Report and Order In the Matter of Fixed and Mobile Services in the Mobile Satellite Service Bands at 1525-1559 MHz and 1626.5-1660.5 MHz". FCC.gov. 6 April 2011. http://hraunfoss.fcc.gov/edocs_public/attachmatch/FCC-11-57A1.pdf. Retrieved 2011-12-13. 
  100. ^ "Federal Communications Commission Table of Frequency Allocations". FCC.gov. 18 November 2011. http://transition.fcc.gov/oet/spectrum/table/fcctable.pdf. Retrieved 2011-12-13. 
  101. ^ "FCC Docket File Number: SATASG2001030200017, "Mobile Satellite Ventures LLC Application for Assignment and Modification of Licenses and for Authority to Launch and Operate a Next-Generation Mobile Satellite System"". FCC.gov. March 1, 2001. pp. 9. http://licensing.fcc.gov/cgi-bin/ws.exe/prod/ib/forms/reports/related_filing.hts?f_key=200647&f_number=SATASG2001030200017. 
  102. ^ "U.S. GPS Industry Council Petition to the FCC to adopt OOBE limits jointly proposed by MSV and the Industry Council". FCC.gov. 4 September 2003. http://fjallfoss.fcc.gov/ecfs/document/view?id=6515082621. Retrieved 2011-12-13. 
  103. ^ "Federal Communications Commission Order and Authorization Granting Authority". FCC.gov. 8 November 2004. http://hraunfoss.fcc.gov/edocs_public/attachmatch/DA-04-3553A1.pdf. Retrieved 2011-12-13. 
  104. ^ "Statement of Julius P. Knapp, Chief, Office of Engineering and Technology, Federal Communications Commission". gps.gov. 15 September 2011. pp. 3. http://www.gps.gov/congress/hearings/2011-09-HASC/knapp.pdf. Retrieved 2011-12-13. 
  105. ^ "FCC Order, Granted LightSquared Subsidiary LLC, a Mobile Satellite Service licensee in the L-Band, a conditional waiver of the Ancillary Terrestrial Component "integrated service" rule". Federal Communications Commission. FCC.Gov. 26 January 2011. http://hraunfoss.fcc.gov/edocs_public/attachmatch/DA-11-133A1.pdf. Retrieved 2011-12-13. 
  106. ^ "Data Shows Disastrous GPS Jamming from FCC-Approved Broadcaster". gpsworld.com. 1 February 2011. http://www.gpsworld.com/gnss-system/news/data-shows-disastrous-gps-jamming-fcc-approved-broadcaster-11029. Retrieved 10 February 2011. 
  107. ^ "Javad Ashjaee GPS World webinar". gpsworld.com. 8 December 2011. http://www.gpsworld.com/gnss-system/news/javad-ashjaee-discuss-javad-gnss-lightsquared-tech-december-8-webinar-12337. Retrieved 2011-12-13. 
  108. ^ "Federal Communications Commission Report and Order In the Matter of Fixed and Mobile Services in the Mobile Satellite Service Bands at 1525-1559 MHz and 1626.5-1660.5 MHz". FCC.gov. 6 April 2011. http://hraunfoss.fcc.gov/edocs_public/attachmatch/FCC-11-57A1.pdf. Retrieved 2011-12-13. 
  109. ^ "FCC Order permitting mobile satellite services providers to provide an ancillary terrestrial component (ATC) to their satellite systems". Federal Communications Commission. FCC.gov. 2003-02-10. http://hraunfoss.fcc.gov/edocs_public/attachmatch/FCC-03-15A1.pdf. Retrieved 2011-12-13. 
  110. ^ "Federal Communications Commission Fixed and Mobile Services in the Mobile Satellite Service". Federal Communications Commission. FCC.gov. 2010-07-15. http://www.federalregister.gov/articles/2010/08/16/2010-19824/fixed-and-mobile-services-in-the-mobile-satellite-service#p-31. Retrieved 2011-12-13. 
  111. ^ http://saveourgps.org/pdf/SIS_DOD_Response_Statement_08122011.pdf
  112. ^ "Coalition to Save Our GPS". Saveourgps.org. http://saveourgps.org/. Retrieved 2011-11-06. 
  113. ^ Jeff Carlisle (23 June 2011). "Testimony of Jeff Carlisle, LightSquared Executive Vice President of Regulatory Affairs and Public Policy to U.S. House Subcommittee on Aviation and Subcommittee on Coast Guard and Maritime Transportation". http://ssv.cachefly.net/lightsquared/wp-content/uploads/2011/06/LSQ-Testimony-Package.pdf. Retrieved 2011-12-13. 
  114. ^ Julius Genachowski (31 May 2011). "FCC Chairman Genachowski Letter to Senator Charles Grassley". http://www.lightsquared.com/documents/FCC%20Julius%20Genachowski%20letter%20to%20Senator%20Grassley%20-%20May%2031,%202011.pdf. Retrieved 2011-12-13. 
  115. ^ a b Tessler, Joelle (2011-04-07). "Internet network may jam GPS in cars, jets". The Sun News. http://www.thesunnews.com/2011/04/07/2085752/internet-network-may-jam-gps-in.html. Retrieved 2011-04-07. 
  116. ^ Orbital periods and speeds are calculated using the relations 4π²R³ = T²GM and V²R = GM, where R = radius of orbit in metres, T = orbital period in seconds, V = orbital speed in m/s, G = gravitational constant ≈ 6.673×10−11 Nm²/kg², M = mass of Earth ≈ 5.98×1024 kg.
  117. ^ Beidou coverage
  118. ^ "Beidou satellite navigation system to cover whole world in 2020". Eng.chinamil.com.cn. http://eng.chinamil.com.cn/news-channels/china-military-news/2010-05/20/content_4222569.htm. Retrieved 2010-10-15. 
  119. ^ Levin, Dan (2009-03-23). "Chinese Square Off With Europe in Space". China: NYTimes.com. http://www.nytimes.com/2009/03/23/technology/23iht-galileo23.html?_r=1&scp=1&sq=chinese%20europe%20galileo&st=cse. Retrieved 2011-11-06. 
  120. ^ "ASM, News on GIS, GNSS, spatial information, remote sensing, mapping and surveying technologies for Asia". Asmmag.com. http://www.asmmag.com/news/india-to-launch-1st-irnss-satellite-by-december. Retrieved 2009-10-13. 

Further reading

External links

Historical
Operational
In development
GNSS augmentation
Related topics
Longwave
Shortwave
Satellite
Defunct
Systems categories
Systems theory · Systems science · Systems scientists (Conceptual · Physical · Social)
Systems
Theoretical fields
Systems scientists
Pitot-static
Gyroscopic
Navigational
Related topics